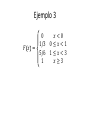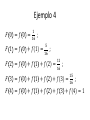Download Distribución discreta de Probabilidades
Document related concepts
Transcript
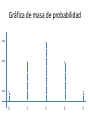
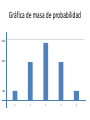
Distribución Discreta de Probabilidad Ing. Raúl Alvarez Guale, MPC Distribución Discreta de Probabilidad El conjunto de pares ordenados (x, f (x)) es una función de probabilidad, una función de masa de probabilidad o una distribución de probabilidad de la variable aleatoria discreta X si, para cada resultado x posible, 1. f (x ) ≥ 0, 2. 𝑥 f (x ) = 1, 3. P (X = x ) = f (x ). Ejemplo 1 Un embarque de 20 computadoras portátiles similares para una tienda minorista contiene 3 que están defectuosas. Si una escuela compra al azar 2 de estas computadoras, calcule la distribución de probabilidad para el número de computadoras defectuosas. Ejemplo 1 Solución: Sea X una variable aleatoria cuyos valores x son los números posibles de computadoras defectuosas compradas por la escuela. Entonces x sólo puede asumir los números 0, 1 y 2. Así, Ejemplo 1 3 𝑓 0 =𝑃 𝑋=0 = 0 17 2 = 68 20 95 2 3 17 51 1 1 𝑓 1 =𝑃 𝑋=1 = = 20 190 2 3 17 3 0 2 𝑓 2 =𝑃 𝑋=2 = = 20 190 2 Ejemplo 1 68/95 𝑓 𝑥 = 51/190 3/190 𝑥=0 𝑥=1 𝑥=2 Ejemplo 2 Si una agencia automotriz vende 50% de su inventario de cierto vehículo extranjero equipado con bolsas de aire laterales, calcule una fórmula para la distribución de probabilidad del número de automóviles con bolsas de aire laterales entre los siguientes 4 vehículos que venda la agencia. Ejemplo 2 Solución: Como la probabilidad de vender un automóvil con bolsas de aire laterales es 0.5, los 24 = 16 puntos del espacio muestral tienen la misma probabilidad de ocurrencia. Por lo tanto, el denominador para todas las probabilidades, y también para nuestra función, es 16. Para obtener el número de formas de vender tres automóviles con bolsas de aire laterales necesitamos considerar el número de formas de dividir 4 resultados en 2 celdas, con 3 automóviles con bolsas de aire laterales asignados a una celda, Ejemplo 2 y el modelo sin bolsas de aire laterales asignado 4 a la otra. Esto se puede hacer de = 4 formas. 0 En general, el evento de vender x modelos con bolsas de aire laterales y 4 - x modelos sin bolsas 4 de aire laterales puede ocurrir de formas, 𝑥 donde x puede ser 0, 1, 2, 3 o 4. Por consiguiente, la distribución de probabilidad f (x) = P(X = x) es: Ejemplo 2 1 4 𝑓 𝑥 = , 𝑝𝑎𝑟𝑎 𝑥 = 0,1,2,3,4 16 𝑥 Función de la distribución acumulativa Definición: La función de la distribución acumulativa F(x) de una variable aleatoria discreta X con distribución de probabilidad f (x) es: 𝐹 𝑥 =𝑃 𝑋≤𝑥 = 𝑓 𝑡 , 𝑝𝑎𝑟𝑎 − ∞ < 𝑥 < ∞ 𝑡≤𝑥 Ejemplo 3 Determinar la función de la distribución acumulativa de: 2/6 𝑥 = 0 𝑓 𝑥 = 3/6 𝑥 = 1 1/6 𝑥 = 3 Ejemplo 3 0 𝑥<0 1/3 0 ≤ 𝑥 < 1 𝐹 𝑥 = 5/6 1 ≤ 𝑥 < 3 𝑥≥3 1 Ejemplo 4 Calcule la función de la distribución acumulativa de la variable aleatoria X de: 1 4 𝑓 𝑥 = , 𝑝𝑎𝑟𝑎 𝑥 = 0,1,2,3,4 16 𝑥 Ejemplo 4 Solución: 1 4 𝑓 𝑥 = , 𝑝𝑎𝑟𝑎 𝑥 = 0,1,2,3,4 16 𝑥 1 4 1 1 4 1 𝑓 0 = = ; 𝑓 1 = = 16 0 16 16 1 4 1 4 3 1 4 1 𝑓 2 = = ;𝑓 3 = = 16 2 8 16 3 4 1 4 1 𝑓 4 = = 16 4 16 Ejemplo 4 𝐹 0 =𝑓 0 = 1 16 ; 𝐹 1 = 𝑓 0 + 𝑓(1) = 5 16 ; 𝐹 2 = 𝑓 0 + 𝑓 1 + 𝑓(2) = 11 16 ; 𝐹 3 = 𝑓 0 + 𝑓 1 + 𝑓 2 + 𝑓(3) = 15 16 ; 𝐹 4 = 𝑓 0 + 𝑓 1 + 𝑓 2 + 𝑓 3 + 𝑓(4) = 1 Ejemplo 4 Por lo tanto: 0, 1/16 5/16 𝐹 𝑥 = 11/16 15/16 1 𝑥<0 0≤𝑥<1 1≤𝑥<2 2≤𝑥<3 3≤𝑥<4 𝑥≥4 Ejemplo 4 Entonces 𝑓 2 = 𝐹 2 − 𝐹(1) 11 5 3 𝑓 2 = − = 16 16 8 Gráfica de masa de probabilidad Graficar: 1 4 𝑓 𝑥 = , 𝑝𝑎𝑟𝑎 𝑥 = 0,1,2,3,4 16 𝑥 Gráfica de masa de probabilidad Solución: 1 4 𝑓 𝑥 = , 𝑝𝑎𝑟𝑎 𝑥 = 0,1,2,3,4 16 𝑥 1/16 4/16 𝑓 𝑥 = 6/16 4/16 1/16 𝑥 𝑥 𝑥 𝑥 𝑥 =0 =1 =2 =3 =4 Gráfica de masa de probabilidad 6/16 4/16 1/16 0 1 2 3 4 Gráfica de masa de probabilidad 6/16 4/16 1/16 0 1 2 3 4 Gráfica de función de la distribución acumulativa 1 3/4 1/2 1/4 0 1 2 3 4 Gracias